Параллельные прямые – это прямые линии, которые лежат в одной плоскости и не пересекаются ни в одной точке. Часто возникает вопрос, имеют ли такие прямые центр симметрии, то есть ось, относительно которой они симметричны.
Центр симметрии – это точка, относительно которой фигура выглядит одинаково, если ее повернуть на 180 градусов. Фигура с центром симметрии обладает особой геометрической симметрией, которая делает ее симметричной и гармоничной визуально.
Таким образом, даже если визуально параллельные прямые могут выглядеть симметричными за счет прямой укладки, математически они не обладают центром симметрии. Однако параллельные прямые имеют свою собственную особенность и красоту, которые активно используются в геометрии и других областях науки.
Имеет ли пара параллельных прямых центр симметрии?

Однако, параллельные прямые могут быть симметричными друг относительно друга. Это означает, что каждая прямая является отражением другой относительно оси, проведенной перпендикулярно к обеим прямым. Такая симметрия называется осевой симметрией. Осевая симметрия позволяет применять определенные преобразования для обеих прямых, сохраняя при этом их взаимное расположение и свойства.
Параллельные прямые: определение и свойства
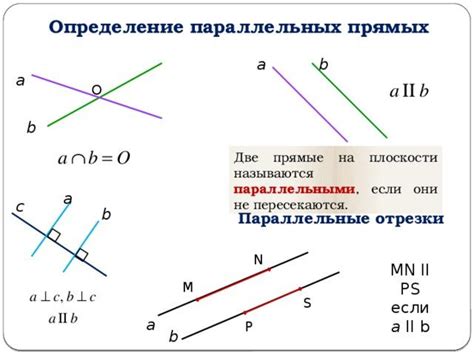
Свойства параллельных прямых:
| Свойство | Описание |
|---|---|
| Однонаправленность | Параллельные прямые имеют одинаковое направление. Если две прямые A и B параллельны, то если продолжить их в том же направлении, они никогда не пересекутся. |
| Расстояние между прямыми | Расстояние между параллельными прямыми всегда одинаково и является постоянным. Это расстояние можно измерить перпендикуляром к одной из прямых. |
| Дополнительные углы | Если две прямые A и B параллельны, а третья прямая пересекает их, то соответствующие углы, вертикальные углы и углы, образованные параллельными прямыми и поперечником, равны друг другу. |
| Транзитивность | Если прямая A параллельна прямой B, а прямая B параллельна прямой C, то прямая A также параллельна прямой C. |
Параллельные прямые широко применяются в геометрии и в различных научных и инженерных областях. Они помогают анализировать и моделировать различные пространственные отношения и свойства.
Симметрия относительно прямой: понятие и особенности
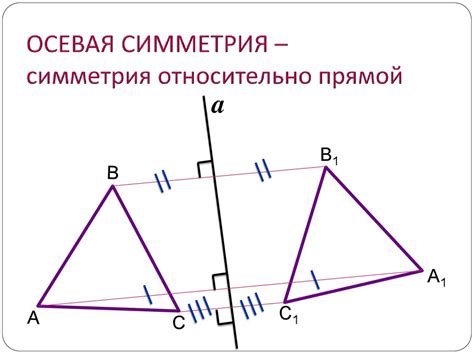
Пара параллельных прямых обладает особой симметрией – симметрией относительно взаимно параллельных прямых. В этом случае, каждая прямая может рассматриваться в качестве оси симметрии для другой прямой.
Основная особенность симметрии относительно параллельных прямых заключается в том, что для каждой точки на одной прямой найдется точка на другой параллельной прямой, такая что они будут симметричны относительно обеих прямых.
Симметрия относительно прямой имеет множество применений в геометрии и в других областях науки. Например, она используется при изучении оптики, конструкции зеркал, компьютерной графики и дизайне. Понимание особенностей этой симметрии позволяет строить сложные геометрические фигуры и находить соответствующие прямые и точки отражения.
Параллельные прямые и их отношение к симметрии
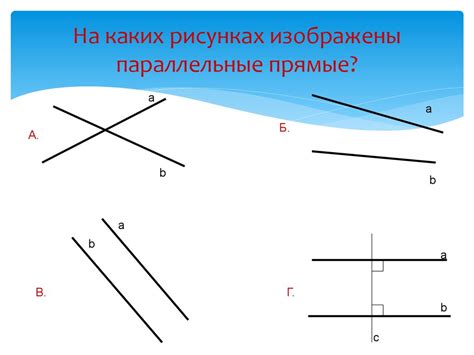
Когда речь идет о симметрии, параллельные прямые имеют особое отношение. Параллельные прямые являются примером осевой симметрии, что означает, что существует прямая, называемая осью симметрии, которая делит фигуру (в данном случае прямые) на две симметричные части.
Примером такой симметричной пары прямых может быть две вертикальные линии, которые находятся на одинаковом расстоянии друг от друга на всей своей протяженности. Ось симметрии будет являться вертикальной линией, проходящей между этими параллельными прямыми.
Параллельные прямые также могут иметь горизонтальную ось симметрии, когда они параллельны горизонтальной линии. В этом случае параллельные прямые будут располагаться на одинаковом вертикальном уровне и иметь одинаковое расстояние друг от друга.
Таким образом, параллельные прямые обладают центром симметрии, который является осью симметрии, и разделяют их на две симметричные части. Это позволяет использовать параллельные прямые в разных математических и геометрических задачах, а также в строительстве и проектировании.
Методы определения центра симметрии
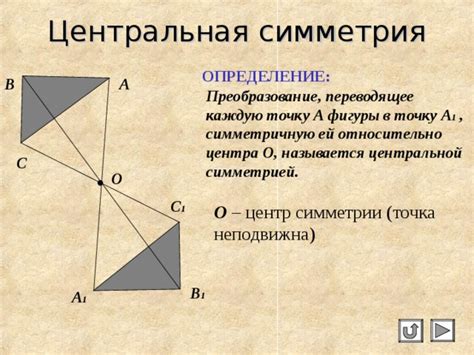
Существует несколько методов определения центра симметрии:
- Геометрический метод: Для определения центра симметрии параллельных прямых можно провести перпендикулярные линии из нескольких точек на одной и другой прямой. Если все эти линии пересекаются в одной точке, то эта точка будет центром симметрии.
- Аналитический метод: Для этого метода необходимо использовать уравнения прямых. Если уравнения параллельных прямых имеют вид y = kx + b1 и y = kx + b2, то центр симметрии может быть найден как точка с координатами (x, y), где x принимает любое значение, а y вычисляется по формуле: y = (b1 + b2) / 2.
- Зеркальность: Если параллельные прямые имеют центр симметрии, то каждая точка одной прямой должна иметь соответствующую симметричную точку на другой прямой. Проверка наличия точек симметрии может быть осуществлена путем отражения одной прямой вдоль другой. Если после отражения прямые полностью совпадают, то они имеют центр симметрии.
Знание методов определения центра симметрии позволяет удобно работать с параллельными прямыми и анализировать их свойства при проведении математических и геометрических исследований.
Симметричные оси: пересечение и параллельность

Центр симметрии - это точка, относительно которой фигура остается неизменной при симметричном отражении. В случае с параллельными прямыми, центр симметрии находится на бесконечности и совпадает с обоими прямыми.
Можно представить параллельные прямые как две бесконечные линии, которые могут быть отражены одна относительно другой. При этом, каждая прямая будет служить центром симметрии для другой прямой.
Это свойство параллельных прямых можно использовать, например, для построения фигур с сохранением их формы. Если мы имеем две параллельные прямые, можно сделать симметричные относительно одной из прямых отражения, и получить новую фигуру, сохраняющую форму и размер.
Таким образом, хотя параллельные прямые не имеют точек пересечения, они обладают центрами симметрии, что является важным свойством при решении геометрических задач.
Доказательство отсутствия центра симметрии у пары параллельных прямых
Предположим, что у пары параллельных прямых есть центр симметрии. Тогда существует ось, относительно которой прямые симметричны. Пусть это будет прямая, перпендикулярная параллельным прямым и проходящая через их середину.
Рассмотрим две точки на параллельных прямых, обозначим их как A и B. Поскольку прямые параллельны, расстояния от этих точек до оси симметрии должны быть равными.
Однако, если мы возьмем точку на одной из прямых, ближе к оси симметрии, и отразим ее относительно этой оси, получим точку, которая будет ближе к другой прямой.
Выходит, что расстояния от точек A и B до оси симметрии не могут быть одинаковыми, что противоречит нашему предположению о существовании центра симметрии у пары параллельных прямых.
Практическое применение параллельных прямых без центра симметрии
Параллельные прямые, не имеющие центра симметрии, имеют широкое практическое применение в различных областях. Ниже приведены некоторые примеры:
- Архитектура и строительство: В строительной индустрии параллельные прямые используются для создания ровных, последовательных и параллельных стен, потолков, полов и других элементов конструкции. Точность и параллельность прямых улучшают внешний вид и качество строительных работ.
- Графика и дизайн: В графическом дизайне и искусстве параллельные прямые используются для создания геометрических узоров, композиций и элементов дизайна. Они могут быть использованы для создания симметричных и сбалансированных композиций, а также для добавления глубины и пространственности в работу.
- Навигация и геодезия: В навигационной и геодезической сферах параллельные прямые используются для измерения расстояний и направлений. Например, на маршрутных картах параллельные прямые могут представлять собой элементы сетки или координатной системы, которые используются для определения маршрутов и точек на карте.
- Проектирование и инженерия: Параллельные прямые широко применяются в инженерии и проектировании, чтобы обеспечить точность и согласованность конструкции. Они могут использоваться для расположения и выравнивания компонентов, перпендикулярных линий, регулировки уровней и многого другого.
Это лишь некоторые примеры применения параллельных прямых без центра симметрии. Их использование может быть найдено во многих других областях, включая механику, электронику, оптику и т.д. В целом, параллельные прямые создают основу для множества практичных и эстетических решений в разных сферах деятельности.



