Иррациональные числа – это числа, которые не могут быть выражены как отношение двух целых чисел. Они характеризуются бесконечной десятичной дробью без периода. Примерами иррациональных чисел являются корень из двух, число Пи и число Эйлера.
Рациональные числа – это числа, которые могут быть представлены в виде отношения двух целых чисел. Они характеризуются конечной или периодической десятичной дробью. К примеру, 1/2, 0.5 и 3 – все это рациональные числа.
Теперь вопрос: может ли иррациональное число быть рациональным? Ответ – нет. По определению, иррациональные числа не могут быть выражены в виде обыкновенной дроби или отношения двух целых чисел.
Можно рассмотреть пример с корнем из двух (√2). Это число является иррациональным, и его десятичное представление будет бесконечным и непериодическим. Если бы √2 было рациональным числом, его можно было бы представить в виде обыкновенной дроби a/b, где а и b целые числа. Но это невозможно, так как √2 иррационально. Таким образом, иррациональное число не может быть рациональным.
Возможно ли иррациональное число быть рациональным
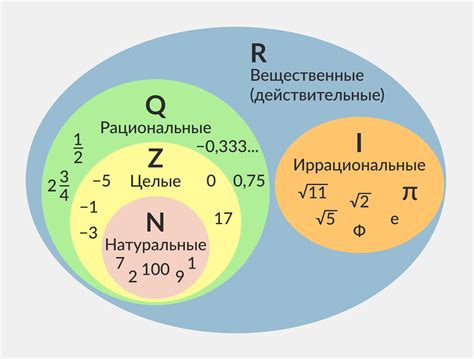
Рациональные числа - это числа, которые могут быть представлены в виде дроби, то есть могут быть выражены в отношении двух целых чисел. Примерами рациональных чисел являются 1/2, -3/4 и 0.25.
В отличие от иррациональных чисел, рациональные числа имеют конечное или повторяющееся количество десятичных знаков. Они могут быть точно представлены с помощью конечного числа цифр или периодическими десятичными знаками.
Таким образом, иррациональные числа и рациональные числа представляют различные типы чисел и не могут быть тождественными. В свою очередь, иррациональные числа являются важной и неотъемлемой частью математических концепций и приложений, таких как геометрия, физика и компьютерная наука.
Определение иррациональных чисел

Пример иррационального числа - корень квадратный из 2. Это число невозможно представить в виде дроби и его десятичная запись продолжается бесконечно без периода: √2 = 1.41421356237...
Другим примером иррационального числа является число "пи" (π), которое представляет отношение длины окружности к ее диаметру. Значение числа "пи" также не может быть точно представлено в виде дроби и его десятичная запись продолжается бесконечно без периода: π = 3.14159265359...
Иррациональные числа имеют важное значение в математике и широко применяются в различных областях, включая физику, инженерию и компьютерные науки.
Рациональные числа и их свойства
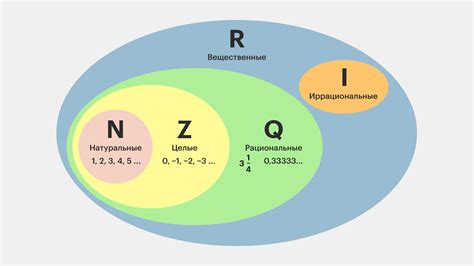
Рациональные числа имеют множество интересных свойств. Среди них:
| Сложение и вычитание | Рациональные числа могут быть складывены и вычитаны друг из друга. При сложении или вычитании рациональных чисел мы можем привести их к общему знаменателю и выполнить операцию над числителями. |
| Умножение и деление | Рациональные числа также могут быть умножены и разделены друг на друга. При умножении рациональных чисел мы умножаем числители и знаменатели отдельно. При делении одного рационального числа на другое, мы умножаем первое число на обратное второму. |
| Порядок чисел | Рациональные числа могут быть упорядочены по возрастанию и убыванию. Мы можем сравнивать и устанавливать отношения между рациональными числами, используя их числительное представление. |
| Десятичное представление | Каждое рациональное число может быть представлено в виде десятичной дроби, которая может быть конечной (например, 0.5) или периодической (например, 0.3333...). |
Рациональные числа являются важным концептом в математике и широко применяются в различных областях, включая финансы, науку, инженерию и многое другое.
Доказательство нерациональности квадратного корня из 2

Тогда можно записать:
| (a/b)2 = 2 |
| a2 / b2 = 2 |
| a2 = 2b2 |
Заметим, что a2 делится на 2 и, следовательно, a также делится на 2. Поэтому a можно представить в виде a = 2k, где k - целое число.
Подставим это выражение для a в исходное уравнение:
| (2k)2 = 2b2 |
| 4k2 = 2b2 |
| 2k2 = b2 |
Заметим, что b2 делится на 2 и, следовательно, b также делится на 2. Поэтому b можно представить в виде b = 2m, где m - целое число.
Подставим это выражение для b в исходное уравнение:
| 2k2 = (2m)2 |
| 2k2 = 4m2 |
Сокращая обе части уравнения на 2, получаем:
| k2 = 2m2 |
Аналогично предыдущему шагу, мы получаем, что k делится на 2. Таким образом, как a, так и b делятся на 2 без остатка.
Однако, это противоречит нашему изначальному предположению, что a и b не имеют общих делителей. Таким образом, наше предположение о том, что квадратный корень из 2 является рациональным числом, неверно. Квадратный корень из 2 является иррациональным числом.



