Пересечение прямых - одна из важнейших задач геометрии. Данная проблема часто возникает при построении и анализе различных фигур. В этой статье мы рассмотрим такую ситуацию: нам дан четырехугольник ABCD, и нам нужно определить, пересекаются ли прямые AC.
Для начала вспомним определение пересечения прямых. Прямые называются пересекающимися, если они имеют общую точку. В нашем случае это точка C, так как мы ищем пересечение прямой AC.
Для определения пересечения прямых мы можем использовать несколько методов. Например, можно воспользоваться геометрической конструкцией или вычислительным методом. Обратите внимание, что точная проверка пересечения может потребовать вычислительных операций, таких как вычисление координат точек пересечения и проверка их совпадения.
Для геометрической конструкции можно использовать компас и линейку. Нам нужно провести прямую AC и убедиться, что она пересекает сторону BD четырехугольника ABCD в точке C. Если прямая AC пересекает сторону BD, то мы можем сказать, что прямые AC пересекаются. Если же прямая AC не пересекает сторону BD, то прямые AC не пересекаются.
Четырехугольник ABCD
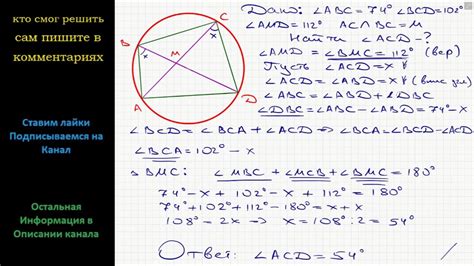
Этот четырехугольник может быть описан разными способами, включая данные о длинах сторон, углах и координатах вершин.
Одним из интересных вопросов, рассматривая четырехугольник ABCD, является взаимное положение диагоналей AC и BD. Прямая AC проходит через точки A и C, а прямая BD - через точки B и D. На самом деле, взаимное положение этих двух прямых зависит от особенностей четырехугольника ABCD. Они могут пересекаться, быть параллельными или даже не пересекаться вовсе.
Положение прямых AC и BD может быть определено с помощью различных методов, включая геометрические и аналитические подходы. Наиболее распространенным методом является использование координат вершин четырехугольника ABCD и решение систем уравнений для определения уравнений прямых AC и BD.
Итак, при изучении четырехугольника ABCD, вопрос о взаимном положении прямых AC и BD является одним из ключевых. Понимание этого положения позволяет детально изучить структуру и свойства данного четырехугольника.
Определение и свойства

Если четырехугольник ABCD выпуклый, то прямая AC не пересекается с остальными сторонами четырехугольника. В этом случае она является отрезком прямой, полностью лежащим внутри четырехугольника, и не имеет точек пересечения с другими сторонами.
Если четырехугольник ABCD невыпуклый, то прямая AC может пересекаться с одной или несколькими сторонами четырехугольника. В этом случае точки пересечения являются общими точками прямой AC и соответствующих сторон четырехугольника.
Свойства прямых AC могут быть использованы для решения различных геометрических задач, связанных с четырехугольниками. Изучение пересечения прямых в четырехугольниках позволяет анализировать их структуру и определять различные их характеристики.
Прямые AC и BD
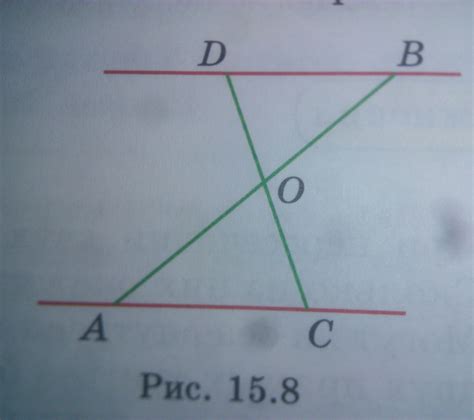
Рассмотрим четырехугольник ABCD. Необходимо определить, пересекаются ли прямые AC и BD.
Прямые AC и BD пересекаются в точке O, которая является точкой пересечения диагоналей четырехугольника ABCD. Точка O является одновременно и центром окружности, описанной вокруг ABCD.
Пересечение прямых AC и BD

В заданном четырехугольнике ABCD нужно определить, пересекаются ли прямые AC и BD.
Для того чтобы узнать, пересекаются ли прямые AC и BD, необходимо проверить условие пересечения двух прямых. Пересечение прямых AC и BD будет иметь место, если точка пересечения лежит на обоих прямых.
Для определения точки пересечения прямых AC и BD можно воспользоваться системой уравнений прямых:
AC: y = kACx + bAC
BD: y = kBDx + bBD
где kAC и kBD - коэффициенты наклона прямых AC и BD соответственно, bAC и bBD - свободные члены уравнений прямых AC и BD соответственно.
Если точка пересечения прямых AC и BD существует, то ее координаты (x,y) будут удовлетворять системе уравнений:
kACx + bAC = kBDx + bBD
(kAC - kBD)x = bBD - bAC
x = (bBD - bAC) / (kAC - kBD)
Подставив найденное значение x в одно из уравнений прямых, можно найти значение y:
y = kACx + bAC
Далее, если точка (x,y) лежит на обоих прямых, то прямые AC и BD пересекаются.
1. Прямые AC пересекаются только в том случае, если отрезок AB и отрезок CD пересекаются. Если отрезки AB и CD не пересекаются, то их продолжения также не будут пересекаться.
2. Для определения пересечения отрезков можно использовать критерий ориентации точек. Если точки A, B, C, D образуют два треугольника ABC и ACD, то отрезки AB и CD пересекаются, если треугольники имеют противоположную ориентацию.
3. Для упрощения проверки пересечения отрезков можно использовать таблицу, в которой указываются координаты точек A, B, C, D и их ориентации. Таблица помогает систематизировать информацию и провести быструю проверку на пересечение.
4. При анализе четырехугольника ABCD важно учесть также возможные исключительные ситуации, например, когда отрезки AB и CD имеют общую точку.
Таким образом, для определения пересечения прямых AC необходимо проанализировать положение отрезков AB и CD относительно друг друга. Единственное пересечение прямых AC происходит, когда отрезки AB и CD пересекаются. В остальных случаях прямые AC не пересекаются.
| Точка | X | Y | Ориентация |
|---|---|---|---|
| A | xA | yA | ориентация A |
| B | xB | yB | ориентация B |
| C | xC | yC | ориентация C |
| D | xD | yD | ориентация D |



