Треугольник - это одна из основных геометрических фигур, состоящая из трех отрезков, соединяющих три различные точки, называемые вершинами. Важно понять, что не все комбинации трех точек могут образовать треугольник. Для проверки существования треугольника необходимо учесть несколько правил и условий.
Одним из основных условий является то, что сумма длин двух сторон треугольника должна быть больше длины третьей стороны. Другими словами, для треугольника ABC длины отрезков AB + BC должны быть больше длины отрезка AC, AB + AC должны быть больше BC, и BC + AC должны быть больше AB.
Для определения существования треугольника по координатам точек A(x1, y1), B(x2, y2) и C(x3, y3) можно использовать формулу расстояния между двумя точками. Для примера возьмем сторону AB. Расстояние между точками A и B можно вычислить по формуле: √((x2 - x1)^2 + (y2 - y1)^2). Если сумма длин дугих двух сторон треугольника также удовлетворяет условиям, то треугольник существует.
Как определить треугольник по координатам
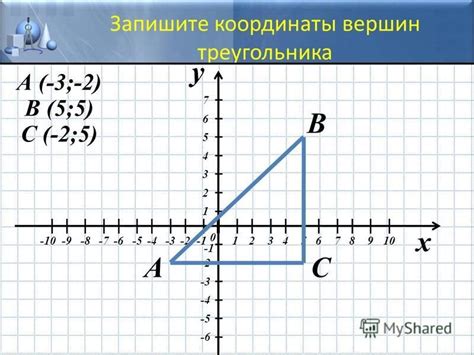
Для определения существования треугольника по заданным координатам его вершин необходимо учитывать следующие правила:
1. Треугольник существует, если сумма длин двух его сторон всегда больше длины третьей стороны.
2. Проверьте, что все точки не лежат на одной прямой. Для этого вычислите площадь треугольника, образованного заданными точками. Если площадь равна нулю, то все точки лежат на одной прямой и треугольник не существует.
3. Для определения площади треугольника по заданным координатам можно использовать формулу "полупроизведения" или формулу Гаусса.
4. Если треугольник существует, то можно проверить его тип. Например, если все стороны равны, то треугольник является равносторонним, если две стороны равны, то треугольник является равнобедренным.
Используя данные правила, можно определить существование и тип треугольника по заданным координатам его вершин.
Методы нахождения треугольника по координатам
Существует несколько методов определения существования треугольника по заданным координатам его вершин.
1. Метод длин сторон: Данный метод основан на использовании формулы расстояния между двумя точками в декартовой системе координат. Если длины всех трех сторон заданного треугольника больше нуля, то треугольник существует.
2. Метод углов: Этот метод использует формулы для вычисления углов между сторонами треугольника по его координатам. Если сумма всех трех углов равна 180 градусов, то треугольник существует.
3. Метод векторного произведения: Векторное произведение двух векторов, образованных сторонами треугольника, позволяет определить, лежат ли точки треугольника на одной прямой или нет. Если векторное произведение нулевое и все стороны не равны нулю, то треугольник существует.
Важно отметить, что все эти методы могут быть использованы только для плоских треугольников в декартовой системе координат.
Анализ длин сторон треугольника

При определении существования треугольника по заданным координатам важно провести анализ длин его сторон. Для этого необходимо вычислить расстояния между точками с помощью формулы расстояния между двумя точками на плоскости:
d = √((x2−x1)^2+(y2−y1)^2)
Полученные значения длин сторон позволяют определить тип треугольника. Если все три стороны имеют одинаковую длину, то треугольник является равносторонним. Если две стороны имеют одинаковую длину, то треугольник является равнобедренным. Если все три стороны имеют разные длины, то треугольник является разносторонним.
Для определения типа треугольника по его длинам можно использовать следующие условия:
- Если все длины равны, то треугольник является равносторонним.
- Если две длины равны, то треугольник является равнобедренным.
- Если все длины разные, то треугольник является разносторонним.
Условие существования треугольника
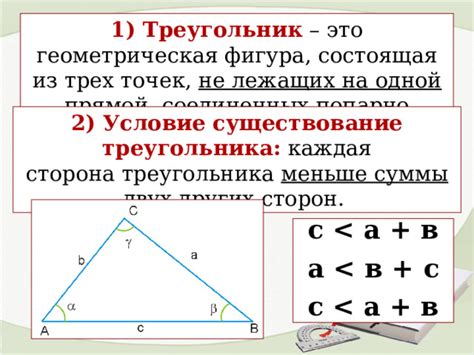
Для того чтобы треугольник существовал, необходимо выполнение следующих условий:
- Никакие две стороны треугольника не могут быть параллельными.
- Сумма длин двух сторон треугольника должна быть больше длины третьей стороны.
- Сумма любых двух углов треугольника должна быть меньше 180 градусов.
Если хотя бы одно из этих условий не выполняется, то треугольник не существует по заданным координатам.
Проверка нахождения точки внутри треугольника

Чтобы проверить, находится ли точка внутри треугольника, можно использовать следующий алгоритм:
- Найдите площадь треугольника, образованного исходными точками A, B и C.
- Разделите эту площадь на три, чтобы получить площадь каждого из трех треугольников, образованных исходными точками и проверяемой точкой P.
- Если сумма площадей трех треугольников, образованных исходными точками и P, равна площади исходного треугольника, то точка P находится внутри треугольника.
- В противном случае, точка P находится вне треугольника.
Этот алгоритм основан на свойстве треугольников: если точка находится внутри треугольника, то сумма площадей трех треугольников, образованных точкой и сторонами треугольника, будет равна площади исходного треугольника.
Применение данного алгоритма позволит определить, находится ли точка внутри треугольника по ее координатам.
Применение теоремы Пифагора для определения треугольника
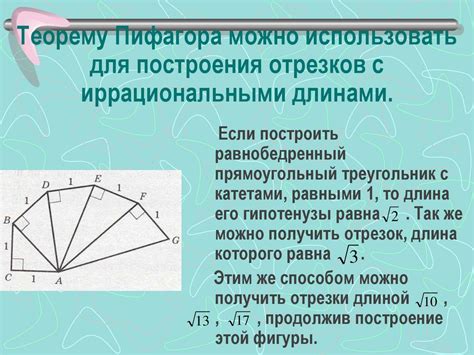
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Если заданные координаты вершин образуют треугольник, то можно рассчитать длины его сторон и проверить, выполняется ли теорема Пифагора для них.
Для этого необходимо:
- Найти расстояние между вершинами A и B, обозначим его AB.
- Найти расстояние между вершинами A и C, обозначим его AC.
- Найти расстояние между вершинами B и C, обозначим его BC.
- Проверить, выполняется ли теорема Пифагора для длин сторон AB, AC и BC. Для этого нужно найти значения квадратов этих длин и проверить, что сумма двух наименьших квадратов равна квадрату наибольшей стороны.
Если теорема Пифагора выполняется для длин сторон треугольника, то треугольник существует. В противном случае, треугольник не существует.
Использование формулы Герона для нахождения площади треугольника

Для определения существования треугольника по его координатам можно использовать формулу Герона для нахождения его площади. Формула Герона основывается на длинах сторон треугольника и позволяет найти его площадь без знания высоты.
Формула Герона выглядит следующим образом:
S = sqrt(p * (p - a) * (p - b) * (p - c))
где:
- S - площадь треугольника;
- p - полупериметр треугольника (сумма длин всех его сторон, разделенная на два);
- a, b, c - длины сторон треугольника.
Если площадь треугольника, найденная с помощью формулы Герона, больше нуля, то треугольник существует. Если площадь равна нулю или отрицательна, то треугольник не существует.



