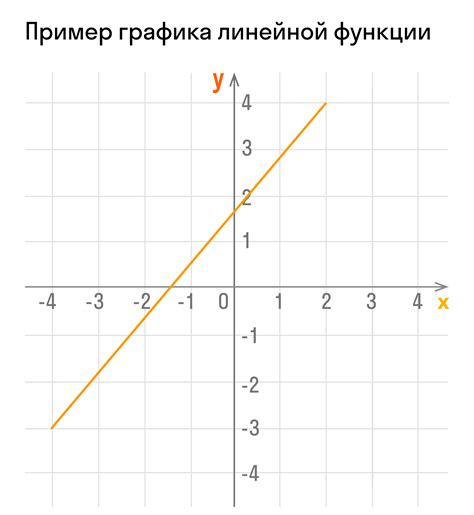
При изучении математики, особенно в рамках алгебры, мы сталкиваемся с различными видами функций. Одним из наиболее простых и понятных видов является линейная функция. График такой функции представляет собой прямую линию на плоскости. Однако возникает вопрос: пересекает ли этот график ось х? В данной статье мы рассмотрим способы проверки этого важного свойства.
Линейная функция задается уравнением вида y = kx + b, где k и b - это константы, которые определяют наклон прямой и ее смещение относительно оси y соответственно. Чтобы узнать, пересекает ли график ось х, необходимо решить уравнение y = 0. То есть нам нужно найти такое значение х, при котором y будет равно нулю. Ведь именно этим характеризуется пересечение графика с осью х.
Для этого решим уравнение: 0 = kx + b. Если решение существует, то график линейной функции пересекает ось х в одной точке. Если решений нет, то график не пересекает ось х. Но как найти значение х? Для этого мы должны избавиться от неизвестного параметра k и выразить х через константы k и b. Если после упрощения уравнения мы получим значение х, значит, график линейной функции пересекает ось х. Если мы не сможем выразить х, значит, значения не существует и график не пересекает ось х. Надеемся, что эта статья поможет вам лучше понять понятие пересечения графика линейной функции с осью х и его проверку.
Что такое проверка пересечения оси х и графика линейной функции?

Для проверки пересечения оси х и графика линейной функции необходимо решить уравнение функции, приравняв ее к нулю. Точка пересечения с осью х будет являться решением этого уравнения и будет представлять собой значение аргумента функции, при котором она обращается в ноль.
Уравнение линейной функции имеет вид: y = ax + b, где a - коэффициент наклона прямой, а b - свободный член, определяющий смещение прямой относительно оси y.
Решение уравнения функции сводится к нахождению значения аргумента, при котором y равняется нулю. Для этого необходимо приравнять уравнение к нулю и решить полученное линейное уравнение относительно x. Полученное значение x будет представлять собой точку пересечения графика с осью х.
Проверка пересечения оси х и графика линейной функции является важным инструментом при исследовании функций, так как позволяет определить точку, в которой функция обращается в ноль и может иметь особое поведение.
| Пример | Решение |
|---|---|
| Уравнение функции: y = 2x - 3 | Для нахождения точки пересечения с осью х приравняем y к нулю: 0 = 2x - 3 Решаем уравнение: 2x - 3 = 0 x = 1.5 Точка пересечения: (1.5, 0) |
Определение и суть пересечения оси х и графика линейной функции
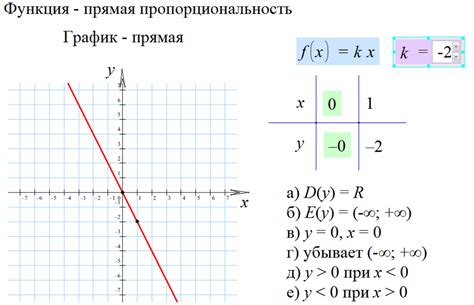
Пересечение оси х и графика линейной функции представляет собой точку или точки, в которых график пересекает горизонтальную ось координат, также называемую осью абсцисс или осью х. В этих точках значение функции равно нулю.
Линейная функция представляет собой функцию вида y = kx + b, где k и b - это константы, а x - независимая переменная (абсцисса). Значение k определяет наклон прямой, а значение b - точку пересечения прямой с осью y (осью ординат или осью у).
Вычисление точек пересечения оси х и графика линейной функции производится путем приравнивания y к нулю и решения уравнения:
0 = kx + b
Отсюда можно определить значение x, в которых график пересекает ось х. Если уравнение имеет один корень (x), то график линейной функции пересекает ось х в одной точке. В случае, когда уравнение имеет два корня (x1 и x2), график пересекает ось х в двух точках.
Пересечение оси х и графика линейной функции играет важную роль в анализе и графическом представлении функций. Оно помогает найти корни уравнения и определить значения переменной x, в которых функция обращается в ноль.
Подходы к выявлению пересечения оси x и графика линейной функции
При анализе графиков линейных функций важно определить точки их пересечения с осью x. Такие точки позволяют нам найти значения аргументов, при которых значение функции равно нулю. Для этого существует несколько подходов.
1. Метод подстановки. Данный метод заключается в подстановке значения 0 в уравнение функции и нахождении соответствующего значения аргумента. Например, если уравнение функции имеет вид y = ax + b, то для того чтобы найти точку пересечения с осью x, мы подставим значение y = 0 и решим полученное уравнение относительно x.
2. Графический метод. Этот метод заключается в построении графика функции и визуальном определении точки пересечения с осью x. Для этого мы просто обращаем внимание на точку, где график пересекает ось x.
3. Алгебраический метод. Для применения данного метода нам нужно решить уравнение функции относительно аргумента x, приравнять его к нулю и найти корни этого уравнения. Это позволит нам определить точки пересечения графика с осью x.
Выбор подхода зависит от конкретной задачи и доступных инструментов для решения уравнений. Важно помнить, что график линейной функции всегда будет иметь пересечение с осью x, так как нулевое значение функции соответствует этой оси.
Метод графического решения задачи пересечения оси х и графика линейной функции
Для решения задачи о пересечении оси OX и графика линейной функции можно использовать метод графического решения. Этот метод основан на построении графика функции и определении точки пересечения с осью OX.
Для начала, нужно записать уравнение линейной функции в виде y = kx + b, где k - коэффициент наклона прямой, а b - свободный член. Значение b будет определять точку пересечения графика с осью OY.
Чтобы построить график функции, нужно выбрать несколько значений для переменной x и вычислить соответствующие им значения y, используя уравнение функции. Затем эти значения записываются в таблицу, где переменной x соответствует столбец, а значениям y - строки.
Полученные точки затем отмечаются на графике, который строится на прямоугольной системе координат. Значение функции для x = 0 даёт точку, в которой график функции пересекает ось OY. Значение x, при котором y = 0, даёт точку пересечения графика с осью OX. Эта точка и есть решение задачи о пересечении оси OX и графика линейной функции.
Метод аналитического решения задачи пересечения оси х и графика линейной функции
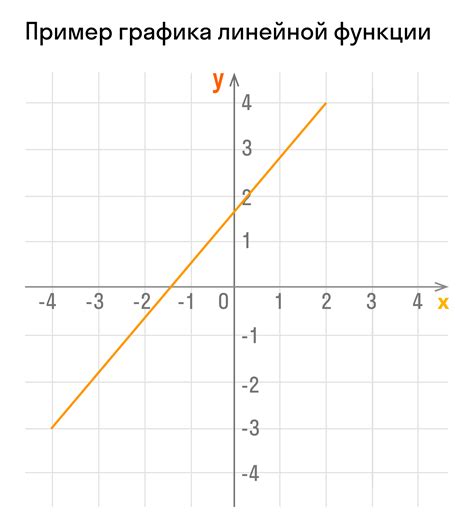
Пересечение оси x и графика линейной функции представляет собой точку или точки, в которых значение функции равно нулю. Для нахождения этих точек можно использовать метод аналитического решения.
Линейная функция представляется уравнением вида y = kx + b, где k - коэффициент наклона, а b - свободный член. Пересечение оси x означает, что значение y равно нулю, поэтому мы можем записать уравнение как 0 = kx + b.
Для нахождения точек пересечения оси x с графиком линейной функции, мы должны приравнять функцию к нулю и решить получившееся уравнение относительно x.
Пример:
Рассмотрим линейную функцию y = 2x - 3. Чтобы найти точки пересечения с осью x, приравняем y к нулю:
0 = 2x - 3
Теперь решим получившееся уравнение относительно x:
2x - 3 = 0
Добавим 3 к обеим сторонам уравнения:
2x = 3
Разделим обе стороны уравнения на 2:
x = 3/2
Таким образом, график линейной функции y = 2x - 3 пересекает ось x в точке (3/2, 0).
Метод аналитического решения позволяет найти точки пересечения оси x и графика линейной функции без необходимости построения графика. Он основан на приравнивании функции к нулю и решении получившегося уравнения относительно x.
Уравнение линейной функции и его влияние на задачу пересечения оси х

Одна из основных задач, связанных с линейной функцией, - найти точку пересечения графика этой функции с осью x. Точка пересечения с осью x называется корнем уравнения и имеет координаты (x, 0). Для нахождения корней уравнения линейной функции нужно приравнять значение y к 0 и решить получившееся уравнение.
- Если уравнение линейной функции имеет вид y = kx + b и k ≠ 0, то корень уравнения можно найти по формуле x = -b / k. Такой корень означает, что график функции пересекает ось x в точке (-b / k, 0).
- Если уравнение линейной функции имеет вид y = b (то есть k = 0), то в этом случае функция является горизонтальной прямой, параллельной оси x, и не имеет точек пересечения с осью x.
Зная уравнение линейной функции, мы можем определить ее поведение и пересечение с осью x. Это дает нам возможность анализировать различные сценарии и использовать эту информацию для решения задач, связанных с линейными функциями.
Примеры задач на проверку пересечения оси х и графика линейной функции
- Найти корень линейной функции. Для этого необходимо приравнять функцию к нулю и решить полученное уравнение. Если ответ является числом, то это означает, что график функции пересекает ось х в данной точке. Например, если функция задана уравнением y = 2x + 3, то решив уравнение 2x + 3 = 0, получим x = -1.5. Значит, график функции пересекает ось х в точке (-1.5, 0).
- Определение отрезка, на котором функция пересекает ось х. Для этого необходимо проанализировать знак функции на интервалах отрицательных и положительных значений x. Если функция меняет знак с отрицательного на положительный, то график функции пересекает ось х на данном интервале. Например, если функция задана уравнением y = -x + 2, то она имеет отрицательные значения при x < 2 и положительные значения при x > 2. Значит, график функции пересекает ось х на интервале (-∞, 2) и (2, +∞).
Эти примеры задач помогут вам лучше понять процесс проверки пересечения оси х и графика линейной функции. Успехов вам в решении задач по данной теме!
Практическое применение и полезность проверки пересечения оси х и графика линейной функции
Проверка пересечения оси х и графика линейной функции имеет широкое практическое применение и может быть полезной в различных областях. Ниже приведены несколько случаев, где эта проверка может быть важной:
- Решение уравнений. Проверка пересечения оси х и графика линейной функции может помочь в решении уравнений, а именно в поиске корней уравнения. Корень уравнения представляет собой значение переменной, при котором график функции пересекает ось х. Проводя график функции и проверяя пересечение оси х, мы можем определить значения переменной, удовлетворяющие уравнению.
- Определение точек экстремума. При нахождении экстремумов (максимумов и минимумов) функции, пересечение оси х может указывать на точки, в которых функция достигает своего экстремального значения. Если график функции пересекает ось х и изменяет свое направление, то это может указывать на возможные точки экстремума.
- Анализ траекторий движения. Проверка пересечения оси х и графика функции может быть полезна при анализе траекторий движения объектов. Если график функции представляет собой зависимость координаты объекта от времени, то пересечение с осью х может указывать на моменты, когда объект возвращается в исходное положение или пересекает ось x. Это может быть важным с точки зрения изучения движения объекта и его характеристик.
- Определение интервалов возрастания и убывания. Проверка пересечения оси х и графика функции также может помочь в определении интервалов, на которых функция возрастает или убывает. Если график функции пересекает ось х и меняет свое направление, то это указывает на изменение знака производной функции и возможные интервалы возрастания или убывания.



