Пересечение плоскостей – одна из фундаментальных задач в геометрии, которая имеет множество применений в различных областях науки и техники. Определить, пересекаются ли две плоскости по заданному уравнению, может быть важным шагом в решении многих задач. Существуют различные способы определения пересечения плоскостей, включая аналитический, графический и векторный подходы.
Аналитический способ основан на решении системы уравнений для двух плоскостей. Если система имеет ненулевое решение, то плоскости пересекаются. Зная уравнения плоскостей, можно составить систему и применить методы решения систем линейных уравнений, такие как метод Крамера или метод Гаусса.
Графический способ заключается в построении графиков плоскостей на плоскости координат и их визуальном анализе. При этом, если графики пересекаются, то плоскости пересекаются. Этот способ визуально нагляден и может быть полезным для первоначальной оценки пересечения плоскостей.
Векторный способ использует свойства векторов, перпендикулярных плоскостям. Если два таких вектора образуют ненулевой угол, то плоскости пересекаются. Векторные операции также могут быть использованы для определения точки пересечения плоскостей.
Рассмотрим пример. Пусть у нас есть две плоскости с уравнениями: 2x + 3y - z = 5 и x - 2y + 4z = 7. Мы можем использовать аналитический метод, составив систему уравнений и решив ее. Решение системы покажет, что плоскости пересекаются по точке (1, -1, 2). Графический метод также может быть применен: построив графики плоскостей на координатной плоскости, мы увидим их пересечение в указанной точке. Векторный метод позволит нам использовать перпендикулярные плоскостям векторы и векторные операции для определения точки пересечения.
Пересечение плоскостей: понятие и значимость
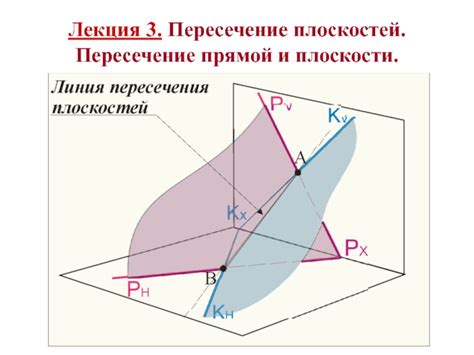
Значимость понятия пересечения плоскостей проявляется во многих областях науки и техники. В геометрии, при изучении трехмерных фигур, знание о взаимном расположении плоскостей позволяет строить сложные модели и анализировать пространственные структуры. В физике, пересечение плоскостей помогает определить точку пересечения траекторий объектов и провести анализ движения. В инженерии, пересечение плоскостей позволяет строить и проектировать сложные конструкции, такие как здания, мосты и машины.
Существуют различные способы определения, пересекаются ли плоскости по уравнению. Один из них – метод решения системы уравнений, составленных из уравнений плоскостей. Если система имеет одно решение, то плоскости пересекаются. Если система не имеет решений, то плоскости не пересекаются. Если система имеет бесконечное количество решений, то плоскости совпадают или лежат в параллельных плоскостях.
Например, рассмотрим плоскости с уравнениями:
Плоскость 1: 2x + 3y - z = 4
Плоскость 2: x - 2y + z = 5
Если решить систему уравнений, получим:
x = 7
y = -1
z = 10
Таким образом, плоскости пересекаются в точке (7, -1, 10).
Геометрический метод определения пересечения плоскостей
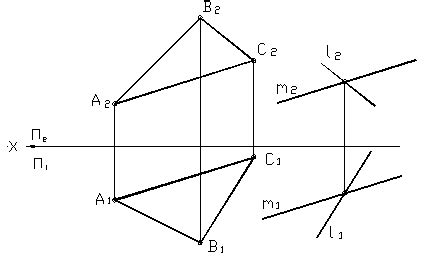
Один из способов определения, пересекаются ли две плоскости, заключается в использовании геометрического метода. Этот метод основан на анализе взаимного расположения плоскостей и линий, в которых они пересекаются.
Чтобы применить геометрический метод, необходимо рассмотреть уравнения данных плоскостей. Представив уравнения векторной форме, можем определить направляющие векторы для каждой плоскости. Затем, для определения пересечения, необходимо найти прямую, лежащую в обеих плоскостях. Эта прямая будет являться линией пересечения и определит, пересекаются ли плоскости.
Для определения прямой пересечения необходимо найти пересечение двух плоскостей. Для этого можно использовать различные методы, например, метод Крамера или метод Гаусса. После нахождения точки пересечения, можно определить направляющие векторы для линии пересечения, которые будут линейной комбинацией направляющих векторов плоскостей.
Пример:
| Плоскость 1 | Плоскость 2 |
|---|---|
| Уравнение: 2x + 3y - z = 4 | Уравнение: x - 2y + z = 6 |
Приведя уравнения к векторной форме, получим:
| Плоскость 1 | Плоскость 2 |
|---|---|
| Уравнение: (2, 3, -1) | Уравнение: (1, -2, 1) |
Найдем прямую пересечения плоскостей. Для этого можно использовать метод Крамера. Решая систему уравнений, получим точку пересечения: (5, -2, -3).
Направляющие векторы прямой пересечения будут линейной комбинацией направляющих векторов плоскостей:
Направляющий вектор линии пересечения - векторное произведение векторов плоскостей:
(2, 3, -1) x (1, -2, 1) = (7, 3, -7)
Таким образом, если найденное направляющее вектор линии пересечения не равен нулевому вектору, то плоскости пересекаются; в противном случае, плоскости параллельны.
Аналитический метод определения пересечения плоскостей
Аналитический метод позволяет определить пересечение плоскостей путем сравнения их уравнений. Для этого необходимо выполнить следующие шаги:
Шаг 1: Записать уравнения плоскостей в общем виде, например, Ax + By + Cz + D1 = 0 и Ex + Fy + Gz + D2 = 0, где A, B, C - коэффициенты при переменных x, y, z, а D1 и D2 - свободные члены.
Шаг 2: Приравнять левые части уравнений плоскостей и избавиться от свободных членов, получив уравнение вида Ax + By + Cz = 0.
Шаг 3: Сравнить коэффициенты при переменных. Если все коэффициенты равны нулю, то плоскости совпадают. Если хотя бы один коэффициент не равен нулю, плоскости пересекаются в пространстве. Если все коэффициенты равны нулю и свободные члены отличаются, плоскости параллельны и не пересекаются.
Например, пусть уравнение первой плоскости - 2x + 3y - 4z + 5 = 0, а уравнение второй плоскости - 4x - 6y + 8z - 10 = 0. После сравнения коэффициентов при переменных, получаем, что плоскости пересекаются, так как не все коэффициенты равны нулю.
Способы анализа уравнений плоскостей на пересечение
Когда решается задача о пересечении двух плоскостей, необходимо провести анализ уравнений этих плоскостей. Существуют несколько способов определить, пересекаются ли плоскости по уравнению или нет.
- Сравнение коэффициентов: необходимо сравнить коэффициенты при переменных в уравнениях плоскостей. Если все коэффициенты совпадают, то это значит, что плоскости совпадают, а значит пересекаются по уравнению. Если хотя бы один коэффициент отличается, то плоскости не пересекаются.
- Проверка совместности: воспользуйтесь принципом Крамера, чтобы определить, являются ли уравнения совместными. Если система уравнений плоскостей совместна и имеет единственное решение, то плоскости пересекаются. Если система совместна и имеет бесконечное количество решений, то плоскости совпадают. Если система несовместна, то плоскости не пересекаются.
- Вычисление угла: если плоскости имеют одну и ту же нормаль, то они будут пересекаться. Чтобы это проверить, нужно вычислить угол между нормалями плоскостей. Если угол равен нулю, то плоскости совпадают и пересекаются.
Зная эти способы анализа уравнений плоскостей на пересечение, вы сможете легко определить, пересекаются ли плоскости по уравнению или нет. Применяйте эти методы, чтобы решать задачи, связанные с пересечением плоскостей.
Определение пересечения плоскостей с помощью системы уравнений
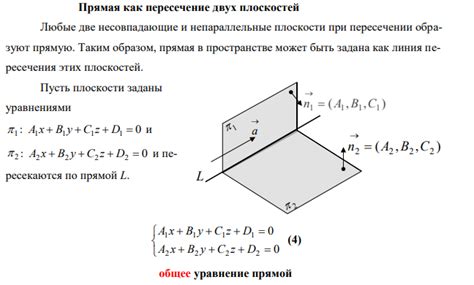
Представим, что у нас есть две плоскости с уравнениями:
Плоскость 1: A1x + B1y + C1z + D1 = 0
Плоскость 2: A2x + B2y + C2z + D2 = 0
Для определения пересечения, необходимо решить систему уравнений, состоящую из этих двух уравнений. Решение системы даст нам точки пересечения этих плоскостей.
Обычно система уравнений решается методами линейной алгебры, такими как метод Гаусса или метод Крамера. После решения системы получаем значения переменных x, y и z, которые являются координатами точки пересечения плоскостей.
Пример:
| Плоскость 1 | 2x + 3y - z + 1 = 0 |
|---|---|
| Плоскость 2 | x + 2y + 5z - 3 = 0 |
Решение системы уравнений даёт значения x = -2, y = 1 и z = 1, то есть точка пересечения плоскостей имеет координаты (-2, 1, 1).
Примеры определения пересечения плоскостей
Существует несколько способов определить, пересекаются ли две плоскости. Рассмотрим несколько примеров, чтобы проиллюстрировать различные ситуации:
| Пример | Уравнения плоскостей | Результат |
|---|---|---|
| Пример 1 | Плоскость 1: 2x + 3y - z = 5 Плоскость 2: x + 2y + 3z = 10 | Плоскости пересекаются |
| Пример 2 | Плоскость 1: 3x - 4y + 2z = 7 Плоскость 2: 6x - 8y + 4z = 14 | Плоскости совпадают |
| Пример 3 | Плоскость 1: x + 2y + 3z = 10 Плоскость 2: 2x + 4y + 6z = 20 | Плоскости параллельны |
| Пример 4 | Плоскость 1: 2x - 3y + z = 5 Плоскость 2: 4x - 6y + 2z = 10 | Плоскости пересекаются в прямой линии |
Это только некоторые примеры для иллюстрации. Определение пересечения плоскостей требует более обширного исследования, включая решение системы уравнений, построение графиков и анализ коэффициентов уравнений.
Решение задач по определению пересечения плоскостей: практические рекомендации
Для начала, необходимо знать уравнения плоскостей. Плоскость обычно задается уравнением вида Ax + By + Cz + D = 0, где A, B и C - коэффициенты уравнения, а D - свободный член. Имея уравнения двух плоскостей, можно попытаться определить, пересекаются ли они.
Существуют несколько способов определения пересечения плоскостей:
1. Метод подстановки:
Простой способ определить пересечение плоскостей - решить систему уравнений плоскостей. Необходимо подставить одно уравнение в другое и решить полученное уравнение относительно одной из переменных (например, x или y). Если полученное уравнение имеет одно решение, то плоскости пересекаются в одной точке; если уравнение имеет бесконечное количество решений, плоскости совпадают; если уравнение не имеет решений, плоскости параллельны и не пересекаются.
2. Метод векторного произведения:
Другой способ определения пересечения плоскостей - вычислить векторное произведение нормалей плоскостей. Если полученный вектор равен нулевому вектору, то плоскости параллельны и не пересекаются. В противном случае, полученный вектор будет нормалью к плоскости, в которой пересекаются исходные плоскости.
3. Готовые формулы для расчета:
Если у вас есть специальные плоскости (например, плоскость, параллельная координатной плоскости), то существуют готовые формулы для определения пересечения с такими плоскостями. Например, плоскость, параллельная оси OX, задается уравнением y = a, где a - константа. Если у вас есть две такие плоскости, то их пересечение будет линией, заданной уравнением y = a.
Важно помнить, что векторы нормалей плоскостей должны быть линейно независимыми для того, чтобы плоскости пересекались.
Примеры:
1. Плоскости с уравнениями x + y + 2z - 3 = 0 и 2x - 3y + z + 5 = 0 пересекаются. Использование метода подстановки позволяет найти точку пересечения: подставляем одно из уравнений в другое и получаем уравнение z = -1, далее подставляем полученное значение z в любое из исходных уравнений и получаем точку пересечения (2, -1, -1).
2. Плоскости x + 2y + 3z - 4 = 0 и 2x + 4y + 6z - 8 = 0 совпадают. Подставляем одно уравнение в другое и получаем тождество 0 = 0, что означает, что плоскости совпадают и имеют бесконечное количество общих точек.
3. Плоскости x + y + z = 0 и x + y + 2z = 0 параллельны и не пересекаются. Нормали к этим плоскостям равны (1, 1, 1) и (1, 1, 2) соответственно. Вычисление векторного произведения нормалей показывает, что полученный вектор (1, -1, 0) не является нулевым вектором, поэтому плоскости параллельны.



